【Python】二重ばね振り子をシミュレーションする

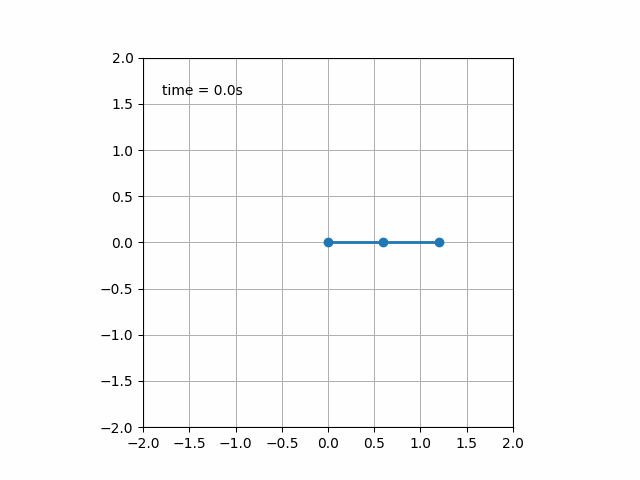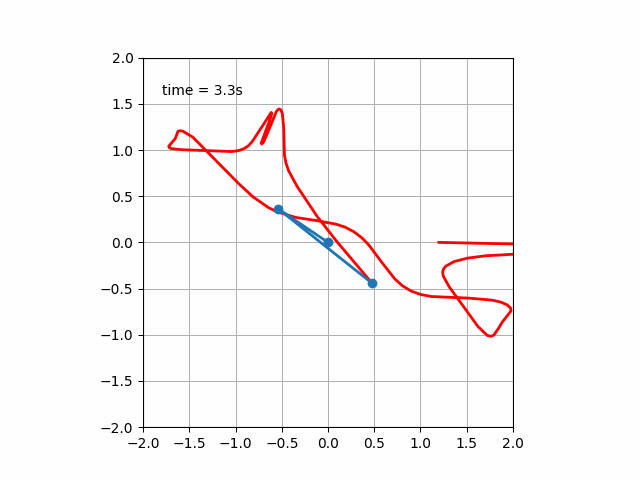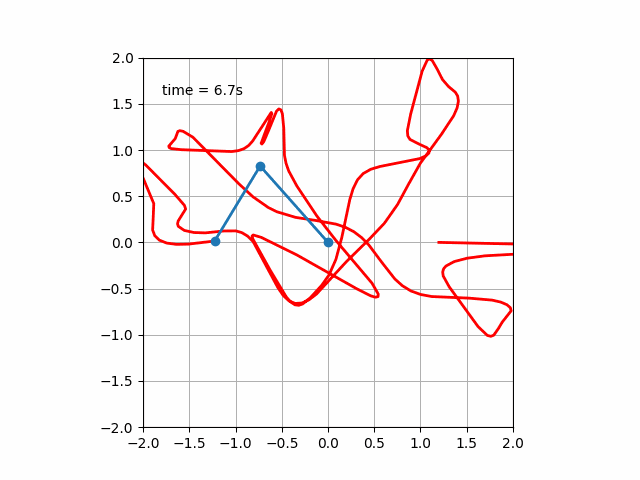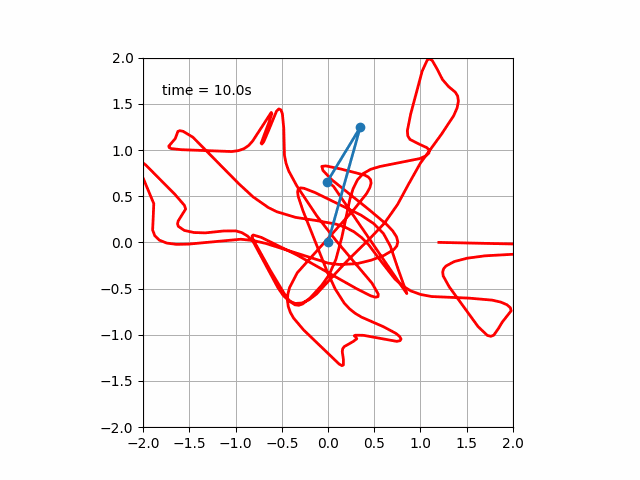
二重ばね振り子の運動方程式をオイラーラグランジュ方程式から導出し、それを基に数値計算を行います。

まずラグランジアンを計算します。図を用意するのが面倒だったので、二重振り子の場合と同様の変数設定をしていると考えてください。ただし質点はばねでつながれていますのでは時間変化します。

運動エネルギーは

\begin{align}
T&=\frac{1}{2}m_1(\dot{x_1}^2+\dot{y_1}^2)+\frac{1}{2}m_2(\dot{x_2}^2+\dot{y_2}^2)\\
&=\frac{1}{2}[m_1[(\dot{l_1}\cos\theta_1-l_1\dot{\theta_1}\sin\theta_1)^2+(\dot{l_1}\sin\theta_1+l_1\dot{\theta_1}\cos\theta_1)^2] \\&+
m_2[(-l_1\dot{\theta_1}\sin\theta_1 - l_2\dot{\theta_2}\sin\theta_2 + \dot{l1}\cos\theta_1 + \dot{l_2}\cos\theta_2)^2 +
(l_1\dot{\theta_1}\cos\theta_1 + l_2\dot{\theta_2}\cos\theta_2 + \dot{l1}\sin\theta_1 + \dot{l_2}\sin\theta_2)^2]]\\
&=\frac{\dot{\theta}_1^{2} l_{1}^{2} m_{1}}{2} + \frac{\dot{\theta}_1^{2} l_{1}^{2} m_{2}}{2} + \dot{\theta}_1 \dot{\theta}_2 l_{1} l_{2} m_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} - \dot{\theta}_1 \dot{l}_2 l_{1} m_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{\theta}_2^{2} l_{2}^{2} m_{2}}{2} + \dot{\theta}_2 \dot{l}_1 l_{2} m_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{l}_1^{2} m_{1}}{2} + \frac{\dot{l}_1^{2} m_{2}}{2} + \dot{l}_1 \dot{l}_2 m_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{l}_2^{2} m_{2}}{2}
\end{align}

ポテンシャルエネルギーは、

\begin{align}
U=-gl_{1} m_{1} \cos{\left(\theta_{1} \right)} - g m_{2} \left(l_{1} \cos{\left(\theta_{1} \right)} + l_{2} \cos{\left(\theta_{2} \right)}\right) + \frac{k_{1} \left(L_{1} - l_{1}\right)^{2}}{2} + \frac{k_{2} \left(L_{2} - l_{2}\right)^{2}}{2}
\end{align}

からラグランジアンが求まります。

これをオイラーラグランジュ方程式に代入して、

\begin{align}
\ddot{\theta_1}&=\frac{L_{2} k_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} - 2 \dot{\theta_1} \dot{l_1} m_{1} - g m_{1} \sin{\theta_{1}} - k_{2} l_{2} \sin{\left(\theta_{1} - \theta_{2} \right)}}{l_{1} m_{1}}\\
\ddot{\theta_2}&=\frac{- L_{1} k_{1} \sin{\left(\theta_{1} - \theta_{2} \right)} - 2 \dot{\theta_2} \dot{l_2} m_{1} + k_{1} l_{1} \sin{\left(\theta_{1} - \theta_{2} \right)}}{l_{2} m_{1}}\\
\ddot{l_1}&=\frac{L_{1} k_{1} - L_{2} k_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} + \dot{\theta_1}^{2} l_{1} m_{1} + g m_{1} \cos{\theta_{1}} - k_{1} l_{1} + k_{2} l_{2} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}}\\
\ddot{l_2}&=- \frac{L_{1} k_{1} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}} + \frac{L_{2} k_{2}}{m_{2}} + \frac{L_{2} k_{2}}{m_{1}} + \dot{\theta_2}^{2} l_{2} + \frac{k_{1} l_{1} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}} - \frac{k_{2} l_{2}}{m_{2}} - \frac{k_{2} l_{2}}{m_{1}}
\end{align}

が得られます。

コードを作成して実行すると次のような運動が見られます。