二重ばね振り子の運動方程式をオイラーラグランジュ方程式から導出し、それを基に数値計算を行います。
まずラグランジアンを計算します。図を用意するのが面倒だったので、二重振り子の場合と同様の変数設定をしていると考えてください。ただし質点はばねでつながれていますのでは時間変化します。
運動エネルギーは
\begin{align}
T&=\frac{1}{2}m_1(\dot{x_1}^2+\dot{y_1}^2)+\frac{1}{2}m_2(\dot{x_2}^2+\dot{y_2}^2)\\
&=\frac{1}{2}[m_1[(\dot{l_1}\cos\theta_1-l_1\dot{\theta_1}\sin\theta_1)^2+(\dot{l_1}\sin\theta_1+l_1\dot{\theta_1}\cos\theta_1)^2] \\&+
m_2[(-l_1\dot{\theta_1}\sin\theta_1 - l_2\dot{\theta_2}\sin\theta_2 + \dot{l1}\cos\theta_1 + \dot{l_2}\cos\theta_2)^2 +
(l_1\dot{\theta_1}\cos\theta_1 + l_2\dot{\theta_2}\cos\theta_2 + \dot{l1}\sin\theta_1 + \dot{l_2}\sin\theta_2)^2]]\\
&=\frac{\dot{\theta}_1^{2} l_{1}^{2} m_{1}}{2} + \frac{\dot{\theta}_1^{2} l_{1}^{2} m_{2}}{2} + \dot{\theta}_1 \dot{\theta}_2 l_{1} l_{2} m_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} - \dot{\theta}_1 \dot{l}_2 l_{1} m_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{\theta}_2^{2} l_{2}^{2} m_{2}}{2} + \dot{\theta}_2 \dot{l}_1 l_{2} m_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{l}_1^{2} m_{1}}{2} + \frac{\dot{l}_1^{2} m_{2}}{2} + \dot{l}_1 \dot{l}_2 m_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} + \frac{\dot{l}_2^{2} m_{2}}{2}
\end{align}
ポテンシャルエネルギーは、
\begin{align}
U=-gl_{1} m_{1} \cos{\left(\theta_{1} \right)} - g m_{2} \left(l_{1} \cos{\left(\theta_{1} \right)} + l_{2} \cos{\left(\theta_{2} \right)}\right) + \frac{k_{1} \left(L_{1} - l_{1}\right)^{2}}{2} + \frac{k_{2} \left(L_{2} - l_{2}\right)^{2}}{2}
\end{align}
\begin{align}
\ddot{\theta_1}&=\frac{L_{2} k_{2} \sin{\left(\theta_{1} - \theta_{2} \right)} - 2 \dot{\theta_1} \dot{l_1} m_{1} - g m_{1} \sin{\theta_{1}} - k_{2} l_{2} \sin{\left(\theta_{1} - \theta_{2} \right)}}{l_{1} m_{1}}\\
\ddot{\theta_2}&=\frac{- L_{1} k_{1} \sin{\left(\theta_{1} - \theta_{2} \right)} - 2 \dot{\theta_2} \dot{l_2} m_{1} + k_{1} l_{1} \sin{\left(\theta_{1} - \theta_{2} \right)}}{l_{2} m_{1}}\\
\ddot{l_1}&=\frac{L_{1} k_{1} - L_{2} k_{2} \cos{\left(\theta_{1} - \theta_{2} \right)} + \dot{\theta_1}^{2} l_{1} m_{1} + g m_{1} \cos{\theta_{1}} - k_{1} l_{1} + k_{2} l_{2} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}}\\
\ddot{l_2}&=- \frac{L_{1} k_{1} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}} + \frac{L_{2} k_{2}}{m_{2}} + \frac{L_{2} k_{2}}{m_{1}} + \dot{\theta_2}^{2} l_{2} + \frac{k_{1} l_{1} \cos{\left(\theta_{1} - \theta_{2} \right)}}{m_{1}} - \frac{k_{2} l_{2}}{m_{2}} - \frac{k_{2} l_{2}}{m_{1}}
\end{align}
コードを簡単に書く方法がわからなかったので、今回はscipyのodeintを使用して手動で実装しました。
コードは以下の通りです。
from numpy import sin, cos from scipy.integrate import solve_ivp from matplotlib.animation import FuncAnimation import numpy as np import matplotlib.pyplot as plt import matplotlib.style as mplstyle import math g = 1 #重力加速度 m1 = 0.5 #質点1の質量 m2 = 0.5 #質点2の質量 k1 = 100 #ばね1のばね定数 k2 = 100 #ばね2のばね定数 L1 = 1 #ばね1の自然長 L2 = 1 #ばね2の自然長 # 運動方程式 def derivs(t, state): #state[0]=theta1, [1]=omega1, [2]=theta2, [3]=omega2, [4]=l1, [5]=v1, [6]=l2, [7]=v2 #dydx[0]=theta1, {1}=\dot{omega1}, [2]=theta2, [3]=\dot{omega2}, [4]=l1, [5]=\dot{v1}, [6]=l2, [7]=\dot{v2} dydx = np.zeros_like(state) dydx[0] = state[1] #theta1=omega1 delta = state[0] - state[2] #delta = theta1-theta2 dydx[1] = (L2*k2*sin(delta) - 2 *m1* state[1] * state[5] - m1*g*sin(state[0]) - k2*state[6] * sin(delta))/(m1*state[4]) dydx[2] = state[3] #theta2=omega2 dydx[3] = (-L1*k1*sin(delta)-2*m1*state[3]*state[7]+k1*state[4]*sin(delta))/(m1*state[6]) dydx[4] = state[5] dydx[5] = (L1*k1-L2*k2*cos(delta)+m1*state[1]*state[1]*state[4]+m1*g*cos(state[0])-k1*state[4]+k2*state[6]*cos(delta))/m1 dydx[6] = state[7] dydx[7] = -(L1*k1/m1)*cos(delta)+L2*k2*(1/m1+1/m2)+state[3]*state[3]*state[6]+(k1*state[4]*cos(delta))/m1 - k2*state[6]*(1/m1+1/m2) return dydx t_span = [0,20] dt = 0.01 t = np.arange(t_span[0], t_span[1], dt) # 初期条件 th1 = 90.0 w1 = 0.0 th2 = 90.0 w2 = 0.0 l1 = 180/math.pi * 0.9 v1 = 0 l2 = 180/math.pi * 0.9 v2 = 0 state = np.radians([th1, w1, th2, w2, l1, v1, l2, v2]) sol = solve_ivp(derivs, t_span, state, t_eval=t) y = sol.y a1=1 a2=1 def gen(): for tt, th1, th2, l1, l2 in zip(t,y[0,:], y[2,:], y[4,:], y[6,:]): x1 = l1*sin(th1) y1 = -l1*cos(th1) x2 = l2*sin(th2) + x1 y2 = -l2*cos(th2) + y1 yield tt, x1, y1, x2, y2 fig, ax = plt.subplots() ax.set_xlim(-(a1+a2), a1+a2) ax.set_ylim(-(a1+a2), a1+a2) ax.set_aspect('equal') ax.grid() locus, = ax.plot([], [], 'r-', linewidth=2) line, = ax.plot([], [], 'o-', linewidth=2) time_template = 'time = %.1fs' time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes) xlocus, ylocus = [], [] def animate(data): t, x1, y1, x2, y2 = data xlocus.append(x2) ylocus.append(y2) locus.set_data(xlocus, ylocus) line.set_data([0, x1, x2], [0, y1, y2]) time_text.set_text(time_template % (t)) ani = FuncAnimation(fig, animate, gen, interval=1, repeat=True) plt.show()
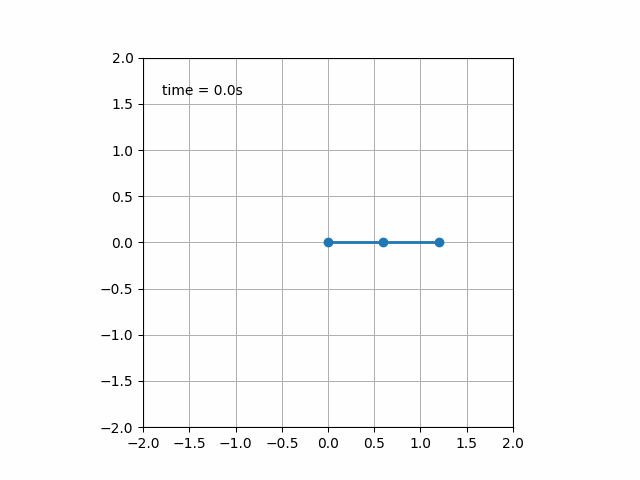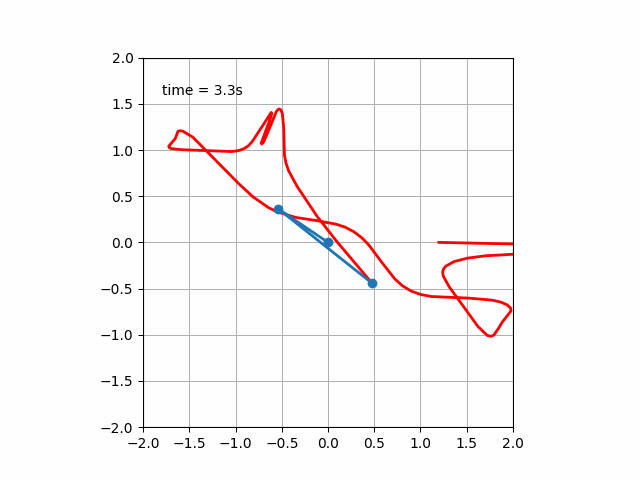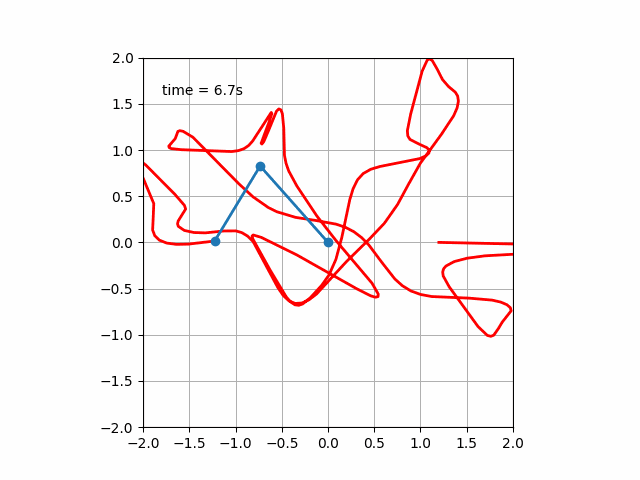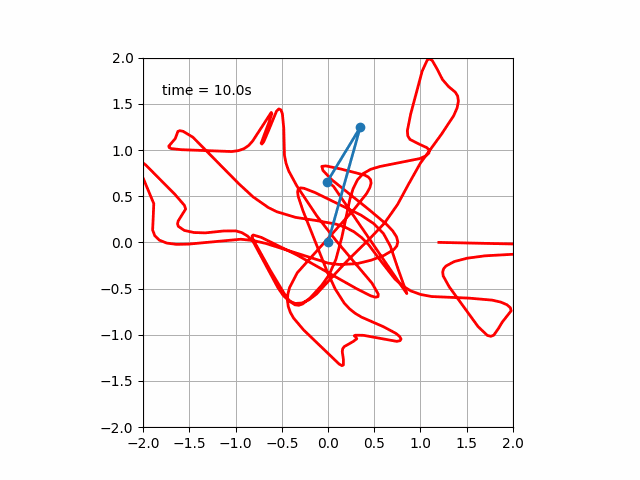
実行すると次のような運動が見られます。